文本数据挖掘

Goal:

extracting information from a usually large amount of different unstructured textual resources. Turn unstructured to structured data.

数据预处理

remove stopwords:

stopwords: frequently occuring and insignificant words.

• a, about, an, are, as…. is, in, of.

stemming

reduce words to their stems or roots.

e.g. computer, computing, compute-> comput

Walks, walker -> walk

Other pre-processing tasks:

Digits removed, hyhens, punctuation marks

Web Page Pre-Processing

针对html不同的部分, \

超链接，超链接代表的内容往往代表了更准确的描述。

移除html tags

Feature re-weighting

并不是所有的词汇是一样重要的，在文档中出现更多的词汇可能相对就缺少discriminatory power。

处理方式： inverse-document frequency

$$IDF = log\frac{n}{d_j}$$

$n$: number of documents

$d_j$: number of documents containing word j.

$Term importance = TF * IDF$

$$tf-idf = f_{ij}\times log(\frac{n}{d_j})$$

$f_{ij}$: term frequency, the relative frequency of word j in document i.

Vector Space Model

Corpus(语料库), a set of N documents

• D =$ {d1,…,dn}$

Vocabulary, a set of M words

• W =${w1,…,w_m}$

$M \times N$的矩阵代表了words的频率

有些词在所有文档里出现很多，但是有的词只在一些文档里出现很多，$tf-idf$就是要惩罚这些出现很多的词。

Query 和 document的相似性计算

余弦相似度: $cos(q,d) = \frac{q^T}{||q||\space ||d||}$

Limitation:

• 维度过高
• 很稀疏，余弦相似度会不准确
• 捕捉不到语义关系，没有关注词汇的内在含义

Topic Modeling

LSA(Latent Semantic Analysis)

pLSA(probabilistic Latent Semantic Analysis)

LDA(Latent Dirichlet Allocation)

概念

words <-> topics(concepts) <->documents

LSA

General Idea

把文档从高维投影到低维，让低维空间反映语言关系，根据向量内积计算document similarity

method：SVD

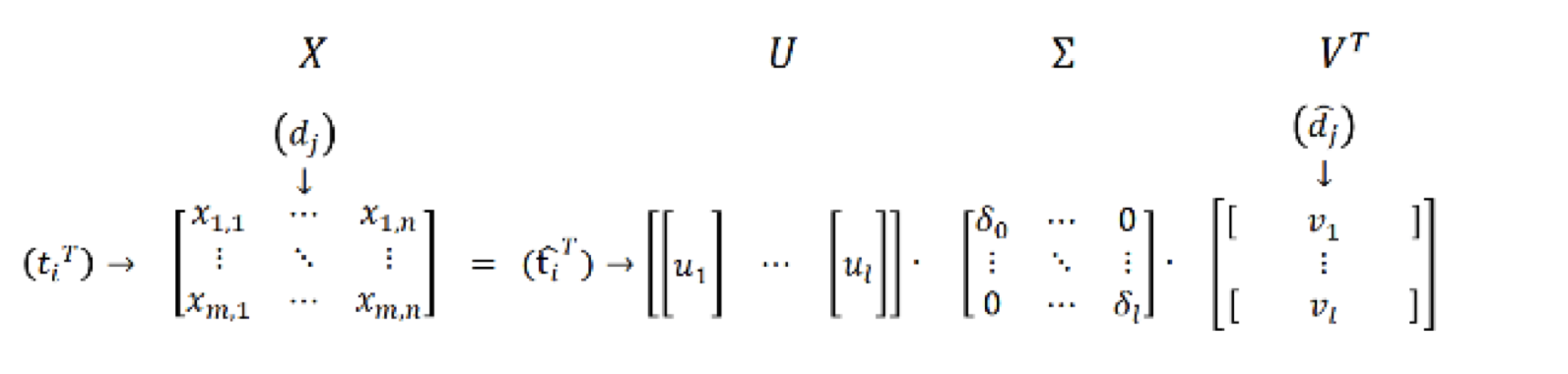
• 给定一个term-document matrix X (m x n)，做奇异值分解。
  • $X=U\sum V^T$
  • 从$\sum$选择k大的奇异值，进行降维。

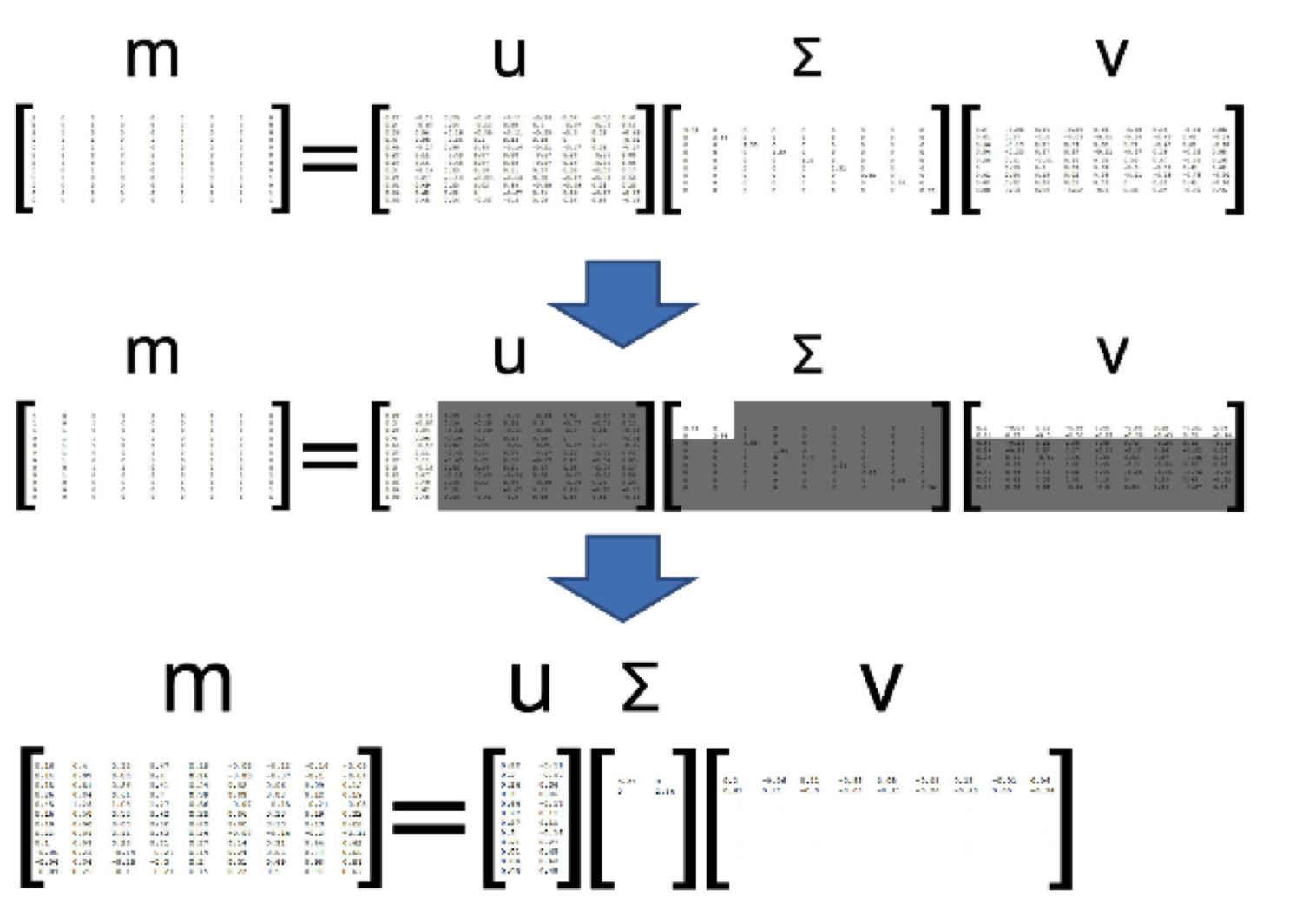
Concept space

降维后我们相当于把原矩阵投影到concept space了，concept ~ topic

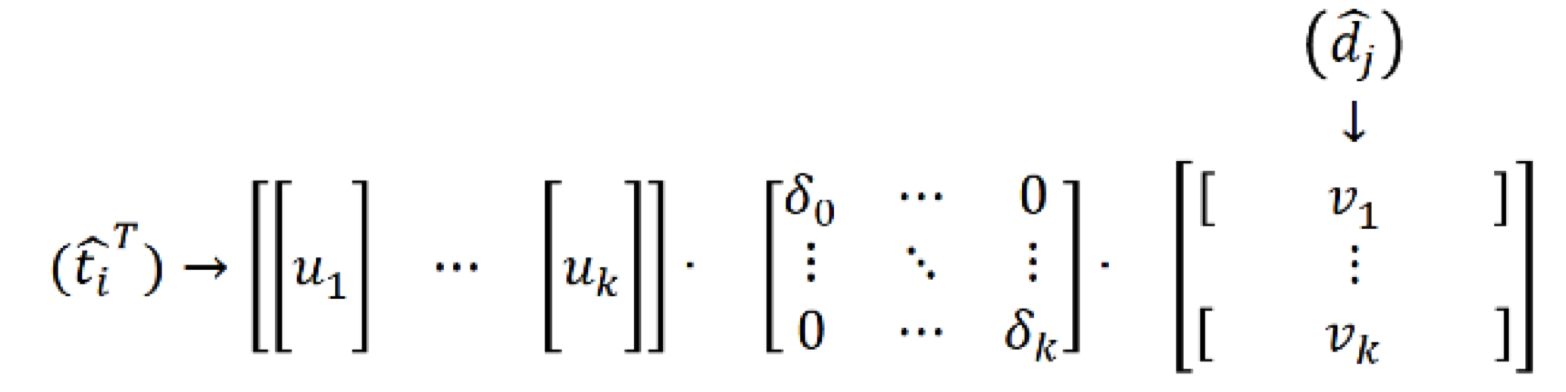
左奇异向量相当于$term_i$在concept空间里的出现。

右奇异向量相当与$document_i$在concept空间里的出现。

计算document q和j的余弦相似度

$$d_j = U_k\sum k \hat d_j$$ $$\hat d_j = {\sum }_k^{-1} U_k ^T d_j$$

Pros and Cons

• Pros
  • 同义词可以被捕捉到
  • 降维可以移除噪声
• Cons
  • 可能有负值，难以解释
  • 一词多义问题无法被解决

pLSA

用概率降维去解决数据稀疏问题？

$$p(d,w)={\sum}_zp(z)p(w|z)p(d|z)$$

• 其中z是latent variable，代表topic.
• $p(d,w)$代表了一个词 w 在一个document d里的概率

有M个document和N个words

• $p(w|z)$：topic z的词分布
• $p(z|d)$：文档d的topic分布
• $p(d,w) =p(d) p(w|d)$
• $p(w|d)={\sum}_zp(w|z)p(z|d)$
• =>$p(d,w)=p(d){\sum}_zp(w|z)p(z|d)$
• $p(d,w)={\sum}_zp(z)p(w|z)p(d|z)$

$p(z), p(w|z), p(d|z)$可以用EM(最大期望)估计。

pLSA 和 LSA的比较

降维过程

• LSA，保留K个奇异值
• pLSA，选取k个topic

和SVD比较

• 左奇异向量U ~ $p(d|z)$, doc to topic
• 右奇异向量V ~ $p(z|w)$, topic to term
• 奇异矩阵$\sum$~$p(z)$, topic strength

pLSA和LSA最主要的区别就是topic的计算。

LDA

(2) implement GetTokenRFScore to get each query token's P(token|feedback model) in feedback documents