SVM理解与推导 (二)

SVM之松弛变量

上文我们说到了SVM的推导，也清楚了我们的目标就是求得使街宽margin最大的hyper plane。那么问题来了，如果数据里存在部分噪声使街宽很小，甚至线性不可分了，这又该怎么办，街宽小了模型缺少泛化能力，而线性不可分了我们必须去引进SVM的kernel了（在下一节会讲到）。

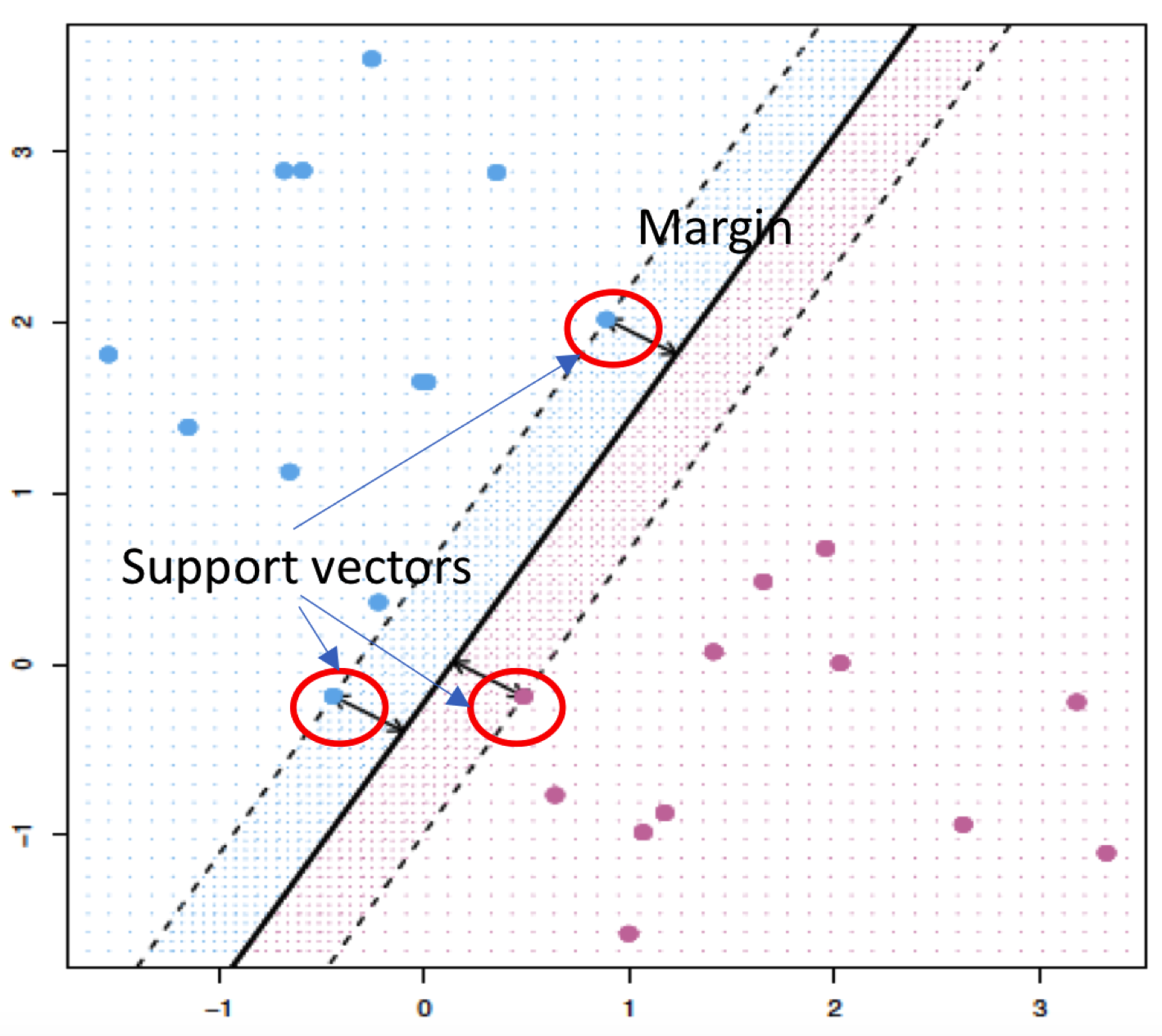
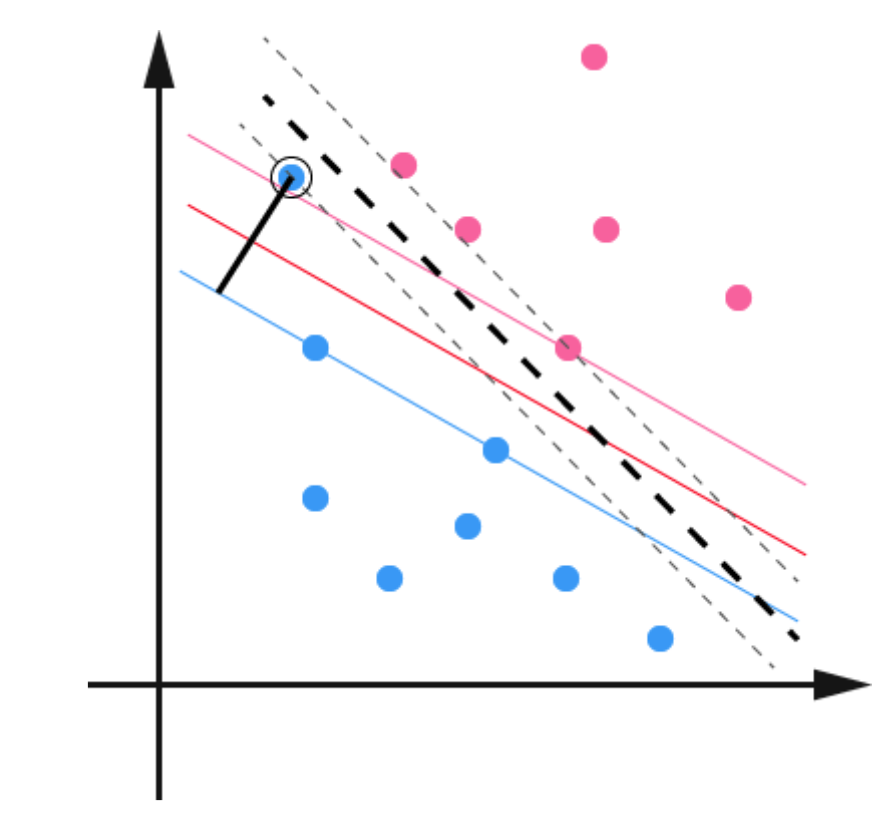
就例如下图被黑线描绘出的蓝点。原本我们的margin（彩色）还是十分美好的，但是加上这个噪音之后，新的margin就变成黑色虚线了，模型的泛化能力一下就差了许多，部分点就会出现分错的情况。

原来的约束条件：

$$y(w^TX+b)\geq1$$

看我们原来的约束条件，如何修改能使这些噪声点不产生如此之大的影响呢？显然我们应该在不等式的右边把这个1变小，且针对每个样本点，右边的值应该是不同的，针对噪声，右边显然应该更小甚至为负数，针对support vector，显然越接近1越好。

因此：

$$y(w^TX+b)\geq1 - \xi_i, \ \ \ \ \ \ \ i = 1,...,n， \xi_i>0$$

其中$\xi_i$就是我们的松弛变量了。那么问题来了，现在的噪音还是我们的support vector吗，回忆之前求街宽的过程，我们就是用支持向量来求的。那么现在我们只需

$$Width =(X^+-X^-)\frac{w}{||w||} \\ =\frac{X^+w}{||w||}-\frac{X^-w}{||w||} \\因为wx=\frac{1-\xi}{y}-b \\Width=\frac{1-\xi-b}{||w||}-\frac{-1+\xi-b}{||w||}=\frac{2-\xi}{||w||}$$

（上述步骤好像在别的地方没有看见过，不知道是不是我搞错了= =）

同理我们要街宽最大，即分母$w$最小，分子$2-\xi$最大，即我们希望$\xi$很小。因此我们得到新的优化问题和约束条件：

$$min\frac{||w||^2}{2}+C\sum^n_{i=1}\xi_i \\s.t. \xi_i>0, \\y(w^TX+b)\geq1 - \xi_i$$

其中C是一个参数，用于控制$\xi$的权重和w的平衡，其实就和正则项很像，不能过大不然这个超平面就根本没用了。

根据拉格朗日函数：

同样的我们可以得到拉格朗日函数：

$$Lmin=\frac{||w||^2}{2}+C\sum^n_{i=1}\xi_i-\sum \lambda _i[y_i(wx_i+b)-1+\xi_i]-\sum^n_{i=1}r_i\xi_i$$

同样求偏导，这次要加一个多$\xi_i$求偏导

$$\frac{\partial L}{\partial w}=w-\sum \lambda _i y_i x_i = 0 \\=> w = \sum \lambda _i y_i x_i \\ \frac{\partial L}{\partial b}=\sum \lambda _i y_i=0 \\ \frac{\partial L}{\partial \xi_i}= 0=> C-\lambda_i-r_i=0$$

我们可知$r_i\geq0,\lambda_i<C$多了一个约束条件

带回原公式（$\xi$可以被消去，太晚了我就先不打公式了溜了有机会再说吧）：

$$Lmin = \sum\lambda_i-\frac{1}{2} \sum^n _{i=1} \sum^n _{j=1} \lambda _i \lambda _j y_i y_j x_i x_j \\ s.t. 0\leq\lambda_i\leq C \\ \sum^n_{i=1}\lambda_i y_i = 0$$

哇发现和之前简直一模一样，就是多了个C而已。

引用july大佬的一段总结：

行文至此，可以做个小结，不准确的说，SVM它本质上即是一个分类方法，用$w^T+b$定义分类函数，于是求$w、b$，为寻最大间隔，引出$1/2||w||^2$，继而引入拉格朗日因子，化为对拉格朗日乘子$\lambda$的求解（求解过程中会涉及到一系列最优化或凸二次规划等问题），如此，求$w.b$与求$\lambda$等价，而$\lambda$的求解可以用一种快速学习算法SMO，至于核函数，是为处理非线性情况，若直接映射到高维计算恐维度爆炸，故在低维计算，等效高维表现。

TODO: 核函数