本文将介绍什么是SVM

SVM是什么？

SVM: support vector machine,俗称支持向量机。是一种二分类模型，其模型定义为特征空间上的间隔最大的线性分类器，策略就是间隔最大化，最终转化为一个凸二次规划问题的求解。感觉已经晕了，下图给出一些intuition的部分:

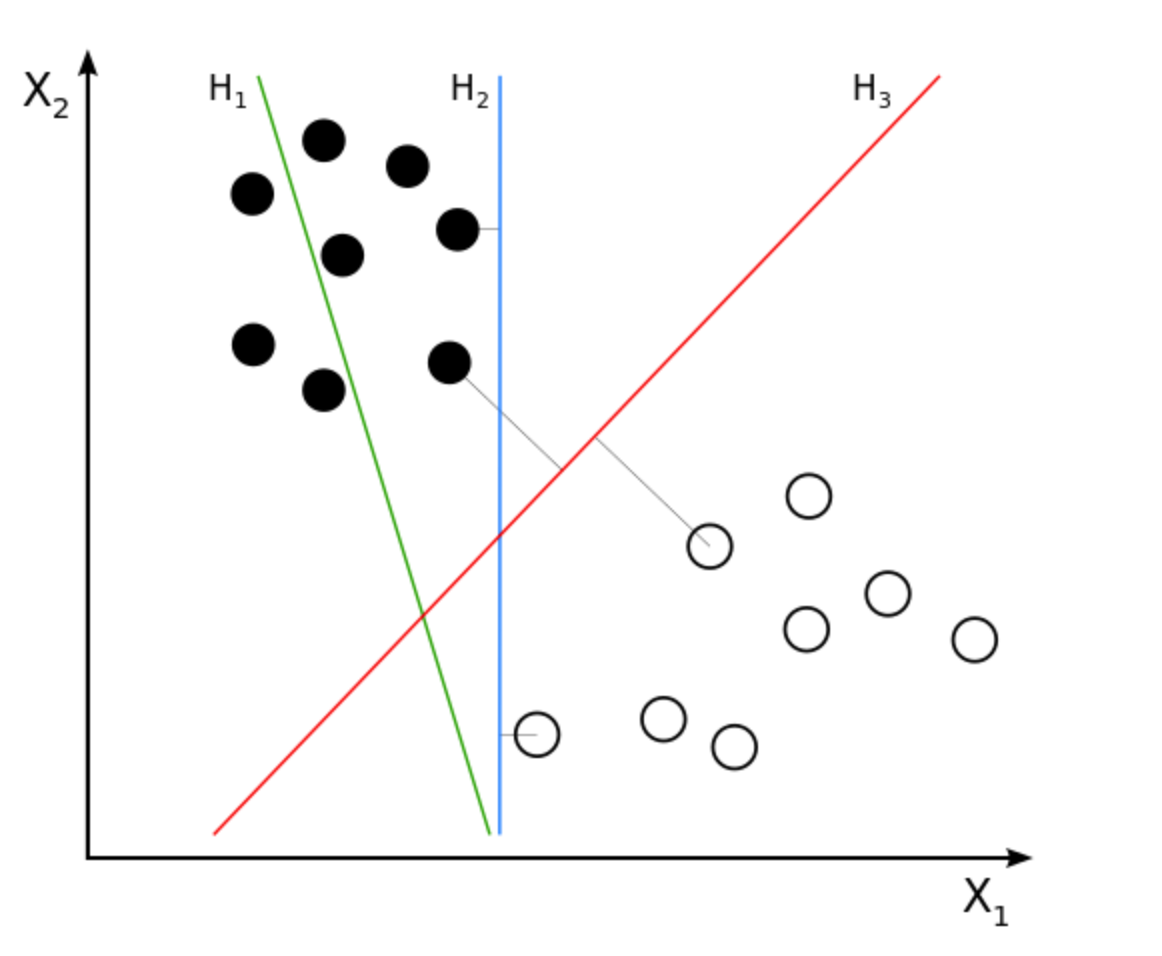
ntution

假设我们有一堆正负样本如图，我们想找一条线（一个超平面）去把这些点分开来。这条线当然是无穷条的，在图中我以H2 和 H3为例，H2和H3看起来都把正负样本分开了，但是我们的目标不是在训练集上取得好成绩吧，我们的目标还包括测试集（unseen data）。

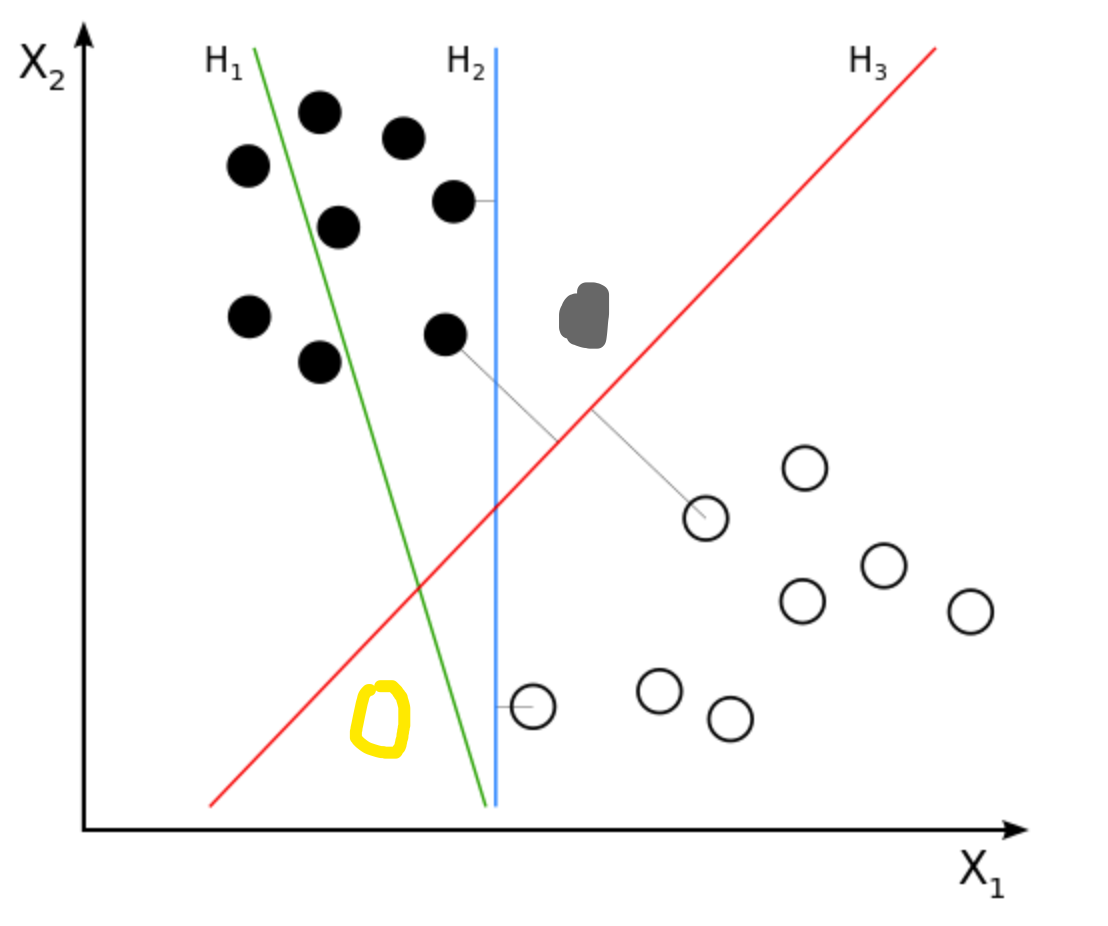
这时候我们给出了测试集（就是我新加上去的点），我们发现H2这条线完全分错了。而H3则分类的不错，粗略得来讲，H3距离正负样本的距离都很远，因此他的泛化能力很强。

至此我们明确了我们的任务，就是找到H3。那么很自然的，我们就产生了两个问题：

如果这样的超平面确实存在，如何寻找？
如果这样的超平面不存在，那么如何找到一个尽可能分开正负样本的超平面？

构造过程

$方法=模型+策略+算法$

回顾之前的方法三要素，我们知道我们的方法要包括模型，策略，算法。即

假设函数$h(\theta)$
损失函数$J(\theta)$
求解方法梯度下降。

那么我们如何在SVM里套用这样的公式呢？我参考了许多网上的推导过程，在SVM里损失函数反而提到的不多，可能也和他的推导过程有关吧。因此在本文，$h(\theta)$和$J(\theta)$将在最后给出。下文将逐步给出SVM的推导过程。

超平面H3的寻找

超平面的定义

首先我们定义超平面为

$H=w^TX+b$

$w,b$是超平面的参数，$X$是样本点。

对超平面的关键假设

在SVM中，我们假设或者可以理解为经过缩放：

$w^TX^++b \geq1$ $w^TX^-+b \leq-1$

*叫做缩放可能更有利于理解。

即一个正样本代入公式，我们希望得出的值$\geq1$，一个负样本代入公式，我们希望得出的值$\leq-1$。而样本代入公式得到的值叫做间隔，该假设（或者叫缩放）称为最大间隔假设。这是SVM里一个很重要的前提，在求解上会提供很大的方便。

支持向量

那么现在我们可以粗略的了解到，在最大间隔假设下，对于训练正样本（注意是训练样本），代入平面公式最小得到的是1，对于训练负样本（注意是训练样本），代入平面公式最大得到的是-1。

因此我们称$w^TX^++b =1$, $w^TX^-+b =-1$的点为Support Vector（支持向量），支持向量就恰好落在这个分界线上，（到现在为止）在训练集中，两边的支持向量中间的街道是没有任何样本点的。

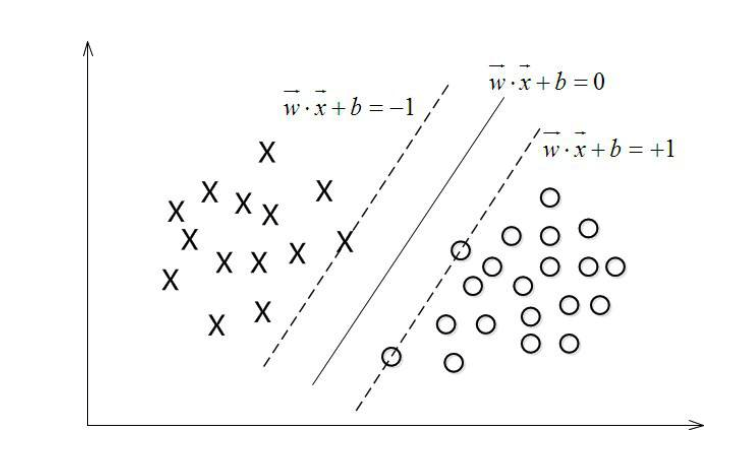
对于支持向量，有如下性质

$y^+(w^TX^++b)=1 * 1 =1$ $y^-(w^TX^-+b)=-1 *- 1 =1$

因此写成一个公式

$y(w^TX+b)=1$

这就是SVM第一个很重要的点。

街道宽度—几何间隔

在之前我们大概了解到，如果中间街道的宽度越大，svm的泛化能力就越好！

那么问题就转移到怎么找$w,b$使得街道的宽度最大了。那么我们现在首先得得到街道的宽度，在SVM里，我们称之为几何间隔。

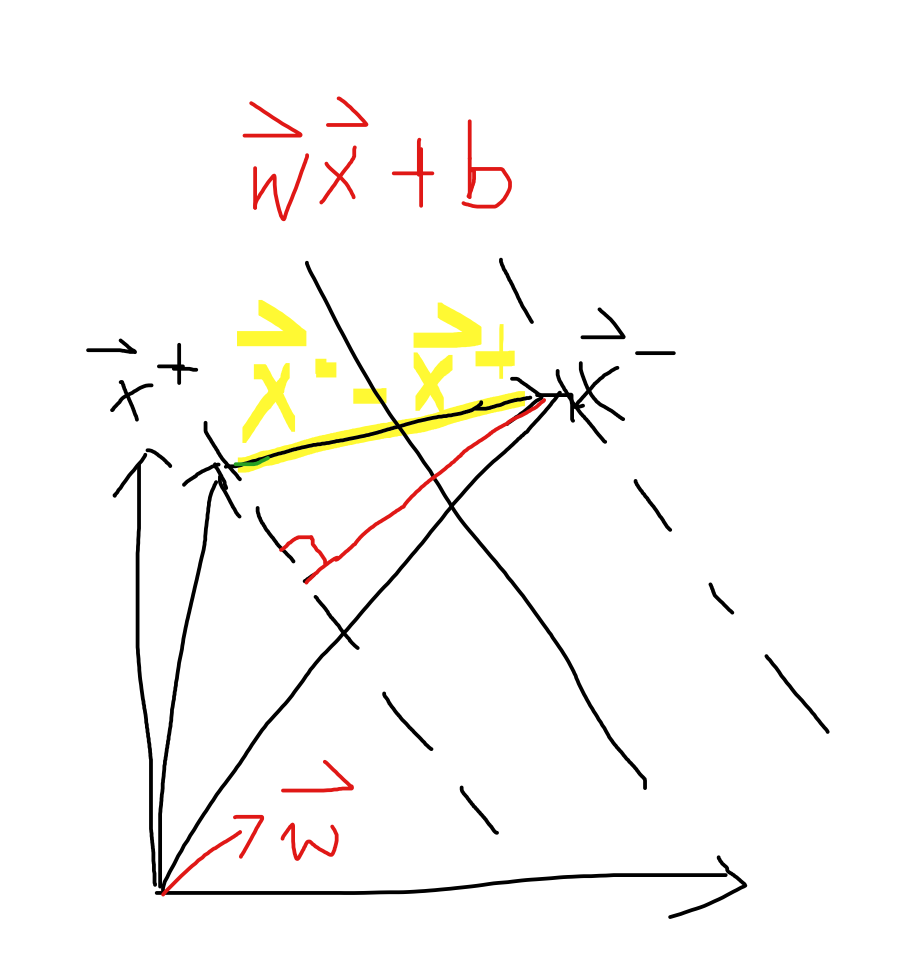
假设我们有两个个样本点$X^+,X^-$，那么可知黄色的向量$X^+-X^-$落在$wx+b=0$的法向量$w$（此处可以百度回忆一下法向量）上的长度就是街宽！因此

$Width =(X^+-X^-)\frac{w}{||w||} \\ =\frac{X^+w}{||w||}-\frac{X^-w}{||w||} \\因为wx=\frac{1}{y}-b \\Width=\frac{1-b}{||w||}-\frac{-1-b}{||w||}=\frac{2}{||w||}$

(此处$X^+,X^-,w$都是向量)。

至此我们得到了几何间隔了，根据我们之前的intuition，我们希望几何间隔最大。

至此，我们得到

$max\frac{2}{||w||} \quad s.t. \quad y(xw+b) = 1 \\同时max\frac{2}{||w||}<=>min||w||<=>min\frac{||w||^2}{2}$

为什么要将$max\frac{2}{||w||} $变成$min\frac{||w||^2}{2}$呢？因为方便求导嘛。现在我们的任务就是求解了。

拉格朗日

现在我们有一个约束条件，$y(xw+b) = 1$，一个优化目标$min\frac{||w||^2}{2}$，使用拉格朗日求解，定义如下：

根据拉格朗日乘子法，我们可以转换我们的问题为：

$L=\frac{||w||^2}{2}-\sum \lambda _i[y_i(wx_i+b)-1]$

对w和b分别求偏导：

$\frac{\partial L}{\partial w}=w-\sum \lambda _i y_i x_i = 0 \\=> w = \sum \lambda _i y_i x_i \\ \frac{\partial L}{\partial b}=\sum \lambda _i y_i=0$

将$\sum \lambda _i y_i=0$, $ w = \sum \lambda _i y_i x_i \$带回$L$，

$L= w =\frac{1}{2} \sum \lambda _i y_i x_i \sum \lambda _j y_j x_j \\ - \sum \lambda _i y_i x_i \sum \lambda _j y_j x_j \\ - \sum \lambda _i y_i b +\sum\lambda_i \\L = \sum\lambda_i-\frac{1}{2} \sum^n _{i=1} \sum^n _{j=1} \lambda _i \lambda _j y_i y_j x_i x_j \\s.t. \sum^n_{i=1}\lambda_i y_i = 0$

我们所要关注的就是如何求解$\lambda$ 了。在这里推荐大家看http://blog.csdn.net/v_july_v/article/details/7624837里的3.5 SMO求解拉格朗日乘子。

TODO:松弛变量、核函数。

你好

SVM理解与推导 (一)