逻辑回归

构造过程

$方法=模型+策略+算法$

回顾之前的方法三要素，我们知道我们的方法要包括模型，策略，算法。即

假设函数$h(\theta)$
损失函数$J(\theta)$
求解方法梯度下降。

假设函数$h(\theta)$

简单介绍：

当我们在针对二分类问题的时候，预测邮件是否为垃圾邮件，肿瘤是否为良性等等，由于我们的预测结果只有0，1，因此这种分类问题我们无法使用线性回归再去预测。

原因：

线性回归要求数据符合正态分布，逻辑回归要求数据符合0，1分布。
线性回归要求$x,y$符合线性关系，逻辑回归则没有要求。
线性回归预测的是分析的是$x,y$的关系，而逻辑回归是分析$y$取某个值的概率与自变量的关系。
线性回归要求$y$是连续变量，逻辑回归要求$y$是离散变量。

$h(\theta)$

逻辑回归的模型是sigmoid function(logistic function)

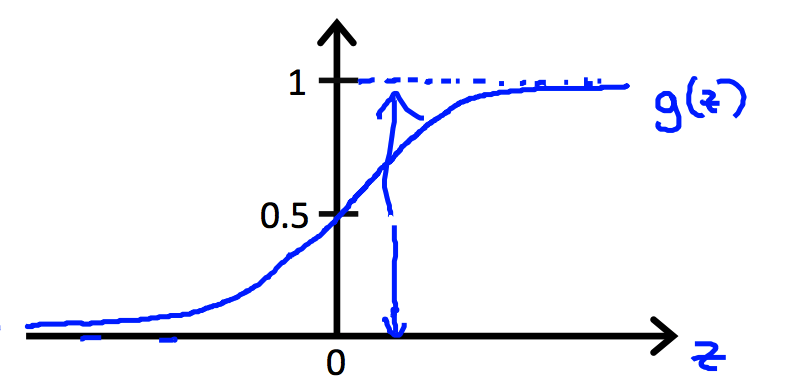
$h_\theta (x) = g(\theta ^T x)=P(y=1|x,\theta)$ $g(z) =\frac{1}{1+e^{-z}}$

我们假设大于0.5时预测值为1，小于0.5时预测值为0。

$P(y=1|x,\theta) =h_\theta (x)$ $P(y=0|x,\theta)=1-h_\theta (x)$

损失函数$J(\theta)$

在上一步中我们得到了如下的公式：

$h_\theta (x)=\frac{1}{1+e^{-\theta^Tx}}$

那么我们要怎么去得到$\theta$呢？

在线性回归中我们得到了一个损失函数，即平方差损失函数

$J(\theta) = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left ( \hat{y}_{i}- y_{i} \right)^2 = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left (h_\theta (x_{i}) - y_{i} \right)^2$

但是这种损失函数应用在逻辑回归里会得到non-convex的结果。

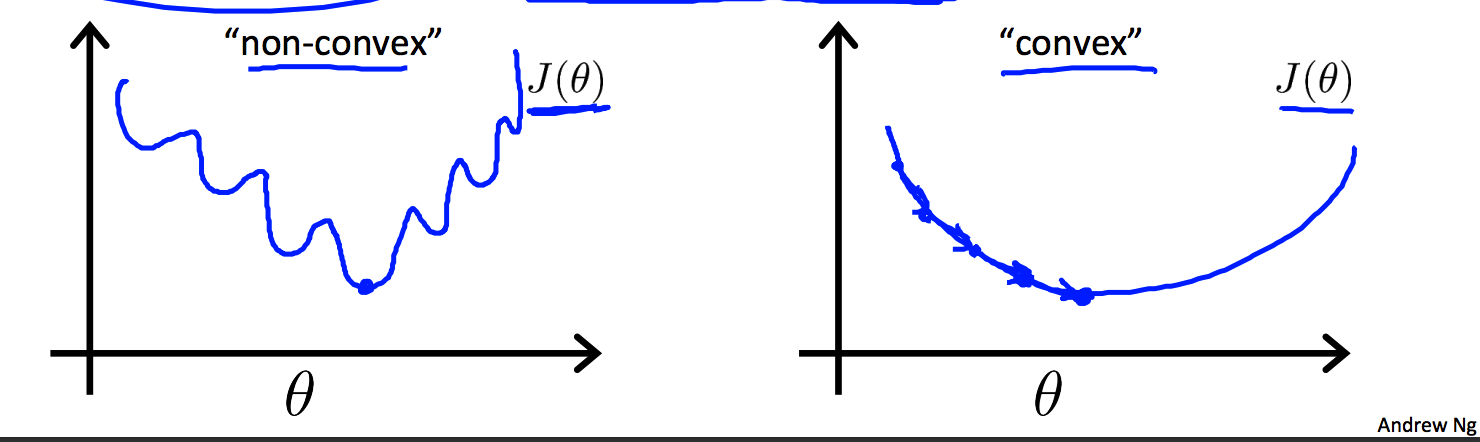
有多个local optimal, 这显然不合理啊。我们期待得到的是一个convex的函数，有global minimum。因此这个不得行，逻辑回归选择了对数损失函数

画出图像如下:

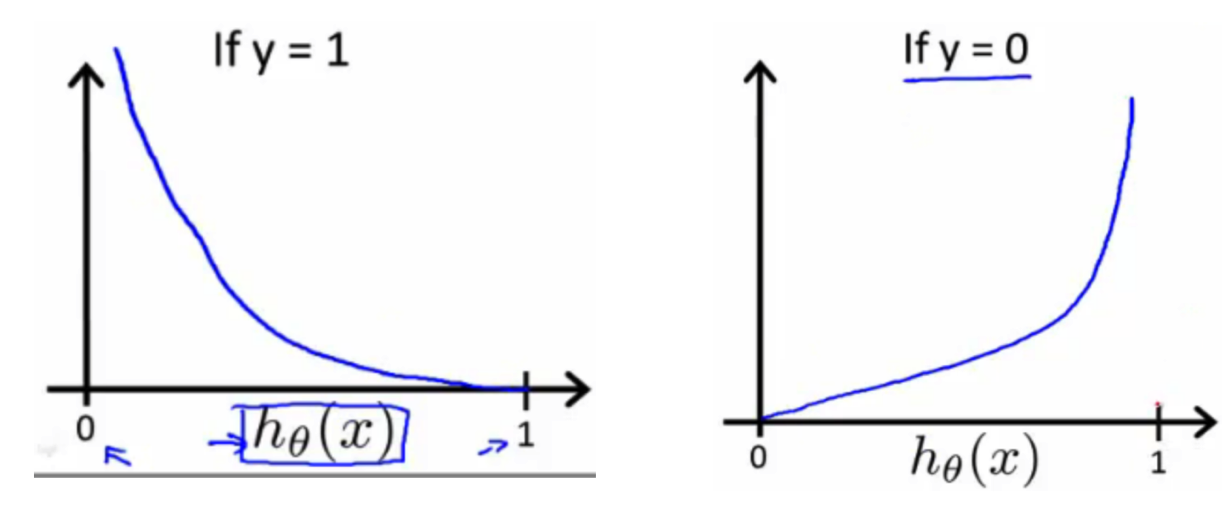
intuition：在y=1时，$h(\theta)$越接近1，损失值越小，当$h(\theta)$接近0时，损失值接近无穷。

在y=0时，$h(\theta)$越接近0，损失值越大，当$h(\theta)$接近1时，损失值接近无穷。

$\begin{align*}& \mathrm{Cost}(h_\theta(x),y) = 0 \text{ if } h_\theta(x) = y \newline & \mathrm{Cost}(h_\theta(x),y) \rightarrow \infty \text{ if } y = 0 \; \mathrm{and} \; h_\theta(x) \rightarrow 1 \newline & \mathrm{Cost}(h_\theta(x),y) \rightarrow \infty \text{ if } y = 1 \; \mathrm{and} \; h_\theta(x) \rightarrow 0 \newline \end{align*}$ $J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))]$

从结果看是很好，很能符合逻辑回归的特点那我们是怎么知道要用这个形式的损失函数的呢？

$J(\theta)$推导过程

$P(y=1|x,\theta) =h_\theta (x) \\P(y=0|x,\theta)=1-h_\theta (x)$

对公式(9)来说，我们可以写成

$P(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}$

intuition：y=1时，预测函数取1的概率，y=0时，预测函数取0的概率。当然这个值我们希望越大越好。

因此取似然函数为，做最大似然估计：

$L(\theta)=\prod ^m_{i=1}(h_\theta(x^i))^{y^{i}}(1-h_\theta(x^i))^{1-y^{i}}$

难以求解，取对数

$l(\theta)=logL(\theta)=\sum ^m _{i=1}(y^i\ logh_\theta (x^i) + (1-y^i)log(1-h_\theta(x^i))$

对比公式(8)，我们发现缺少了1/m，这个好理解，平滑损失值。但是出现了一个负号。这个负号在线性回归的损失函数里是没有的：

$J(\theta) = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left ( \hat{y}_{i}- y_{i} \right)^2 = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left (h_\theta (x_{i}) - y_{i} \right)^2$

其实也可以这么用，不用取负号，使用梯度向上法求解。但是Andrew Ng是加了负号。

个人理解：因为在最大似然函数里，我们求的是使公式值最大的$\theta$的值，但是在损失函数里，我们求得是损失最小值，为了方便我们理解损失函数以及梯度下降，Andrew取了负号。但是本质已经和线性回归不一样了。

于是可得到

$\begin{align*}& J(\theta) = \dfrac{1}{m} \sum_{i=1}^m \mathrm{Cost}(h_\theta(x^{(i)}),y^{(i)}) \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(h_\theta(x)) \; & \text{if y = 1} \newline & \mathrm{Cost}(h_\theta(x),y) = -\log(1-h_\theta(x)) \; & \text{if y = 0}\end{align*}$ $J(\theta) = - \frac{1}{m} \displaystyle \sum_{i=1}^m [y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))]$

梯度下降

$\theta:=\theta-\alpha \frac{d}{d\theta} J(\theta)$

求偏导部分$\alpha \frac{d}{d\theta} J(\theta)$：

因此参数更新：

$\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m{ \left(\frac{1}{1 + e^{-\theta^T x^{(i)}}} - y^{(i)}\right) x_j^{(i)}}(simultaneously \ update \ for \ all \ j)$

对比线性回归，两个方程是一样的，差别在$(h_\theta(x^{(i)})$.

$\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m{ (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)}_j} (simultaneously \ update \ for \ all \ j).$

Python实现

def sigmoid(inX):
    return 1.0/(1+exp(inX))

def gradDesc(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    thetas = ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * thetas)
        error = h - labels
        thetas = thetas - alpha * dataMatrix.tranpose()*error
    return thetas

你好

logistic regression