正则化

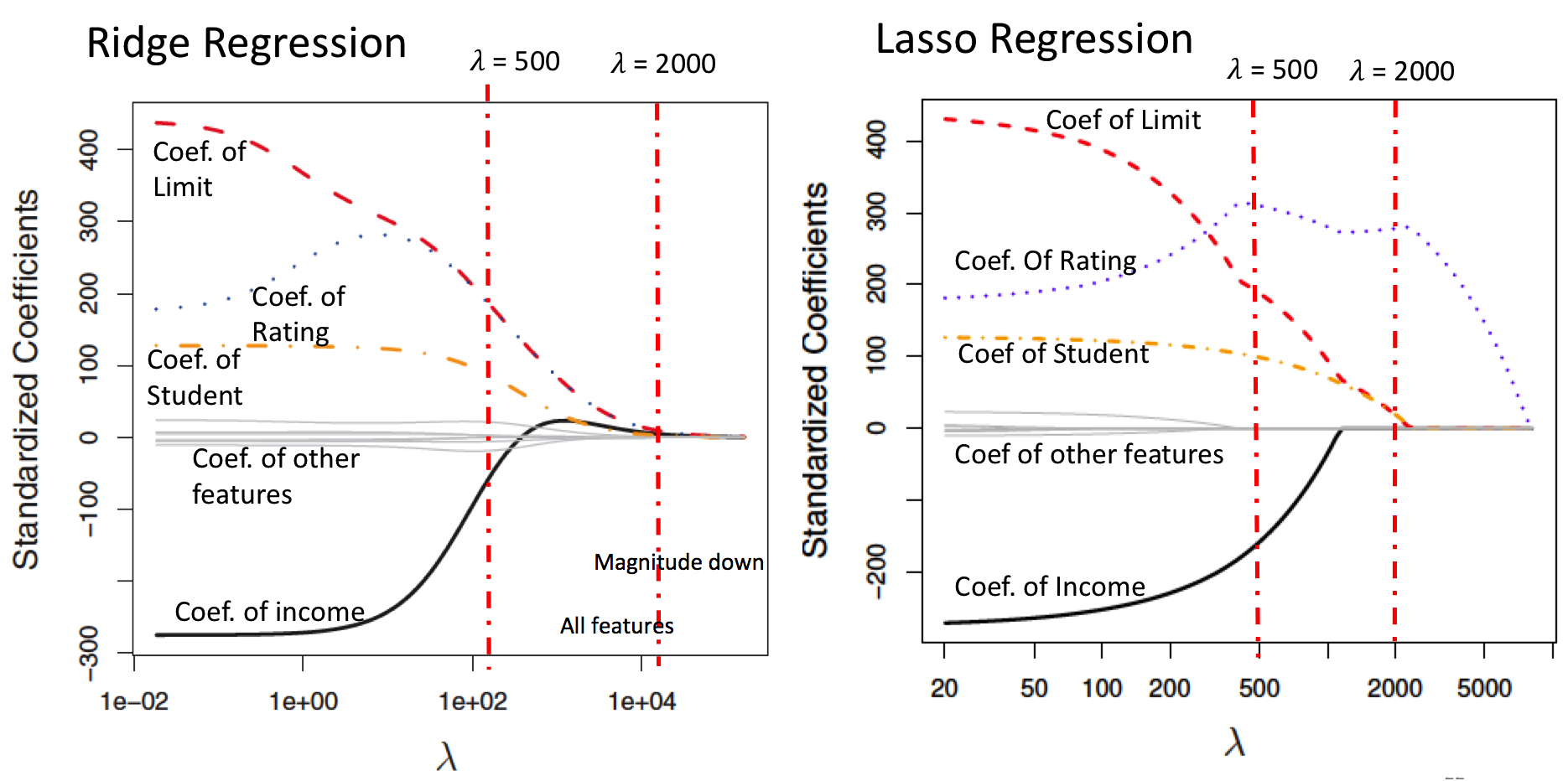
正则化定义

在数据量很少，特征很多的时候，模型往往会表现的过于复杂。bias(训练误差)会降低，但是variance(测试误差)会升高，会产生过拟合的情况。

过拟合为什么不好

比如我们想预测匹兹堡市的年收入情况，但是我们只采访了匹兹堡大学周围的人，没有采访别的人，我们在用这部分数据预测的时候，预测匹兹堡大学周围的生日当然是可以的，但是想预测整个匹兹堡的收入呢？自然不行。数据并没有代表性，或者说数据的有些维度在测试集是可以帮助达到global optimal，但是在unseen dataset中并没有卵用，导致了模型没有泛化能力。

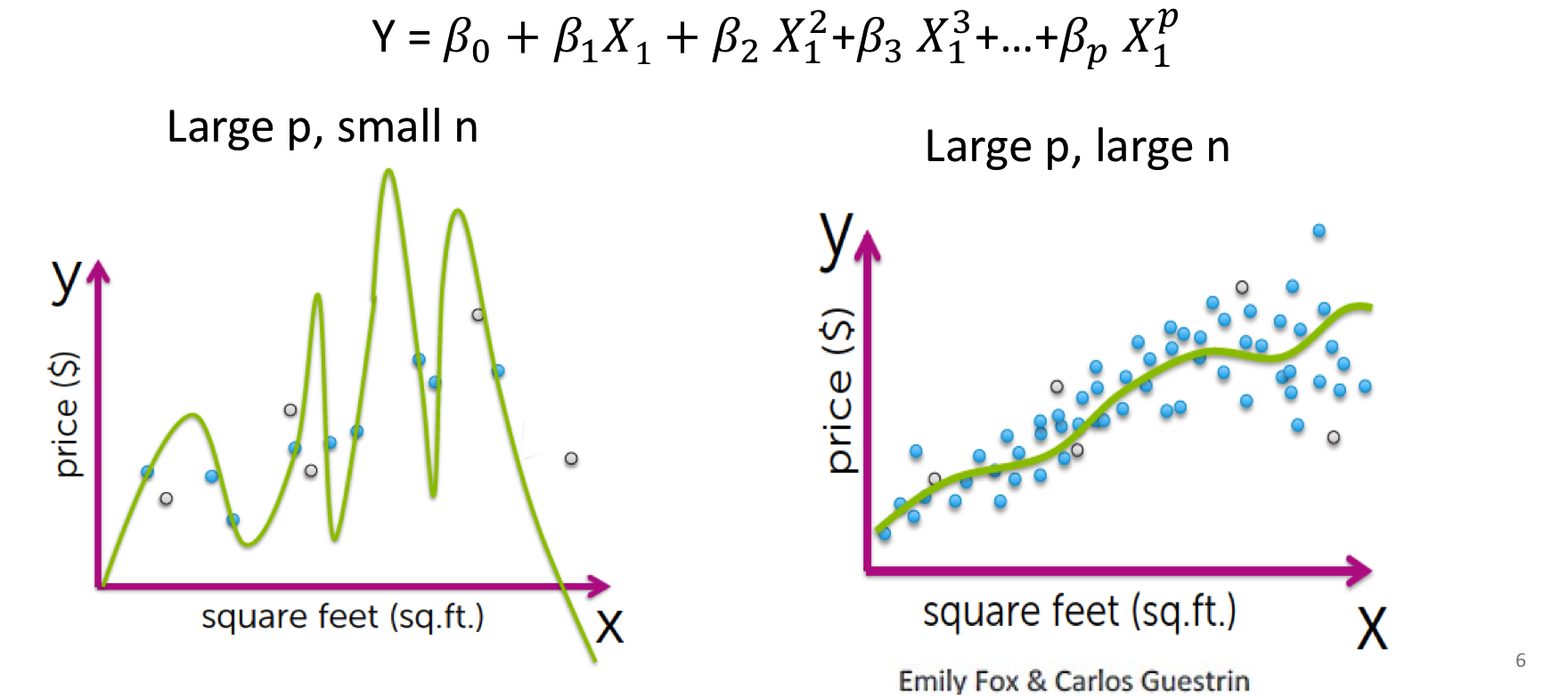
P为特征数，n为样本数。样本数太少，可能造成过拟合

因此我们要在bias和variance之间找一个tradeoff。

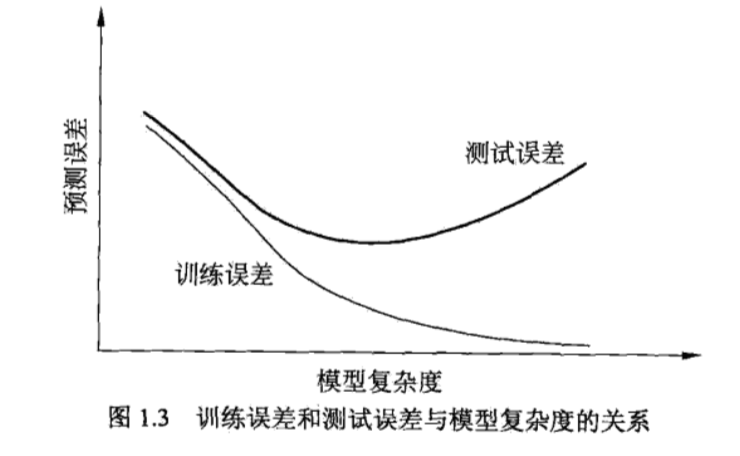
降低模型复杂度有两种方法：

• 减少特征的数量：

  具体而言，我们可以人工检查每一项变量，并以此来确定哪些变量更为重要，然后，保留那些更为重要的特征变量。至于，哪些变量应该舍弃，我们以后在讨论，这会涉及到模型选择算法，这种算法是可以自动选择采用哪些特征变量，自动舍弃不需要的变量。这类做法非常有效，但是其缺点是当你舍弃一部分特征变量时，你也舍弃了问题中的一些信息。例如，也许所有的特征变量对于预测房价都是有用的，我们实际上并不想舍弃一些信息或者说舍弃这些特征变量。

• 降低特征的权重:

  当我们有很多特征变量时，其中每一个变量都能对预测产生一点影响。正如我们在房价预测的例子中看到的那样，我们可以有很多特征变量，其中每一个变量都是有用的，因此我们不希望把它们删掉，这就导致了正则化概念的发生。

正则化一般具有如下形式：

$$min\frac{1}{N}\sum_{i}^{N}{L(y_1,f(x_1)) } + \lambda J(f)$$

第一项是经验风险$R{emp}$，第二项是正则化项$r(d)$，$\lambda \geq 0$为调整两者之间关系的系数. $R{emp}+r(d)$结构风险，正则化就是结构风险最小化的过程。

对于第一项Loss函数，如果是Square loss，那就是最小二乘了；如果是Hinge Loss，那就是著名的SVM了；如果是exp-Loss，那就是牛逼的 Boosting了；如果是log-Loss，那就是Logistic Regression了；

L1vsL2

在正则化项中我们引入了0-2范数：

• 0范数，向量中非零元素的个数。

• 1范数，为绝对值之和（Lasso regularization）

  $$L1=min\frac{1}{N}\sum_{i}^{N}{L(y_1,f(x_1)) } + {\lambda } \left| \left| W \right| \right| _{1}$$

• 2范数，就是通常意义上的模（Ridge Regression），向量各元素的平方和然后求平方根。

$$L2=min\frac{1}{N}\sum_{i}^{N}{L(y_1,f(x_1)) } + {\lambda } \left| \left| W \right| \right| _{2} ^{2}$$

L1,L2特点

L1范数会将所有特征的参数shrinka接近0，会选择出关键的特征，便于解释模型，但在梯度下降求偏导中会有点麻烦（绝对值）。

L2范数会将部分参数接近0，从学习理论的角度可以防止过拟合，提高模型的泛化能力，求偏导简单（似乎因此更popular）。

梯度下降

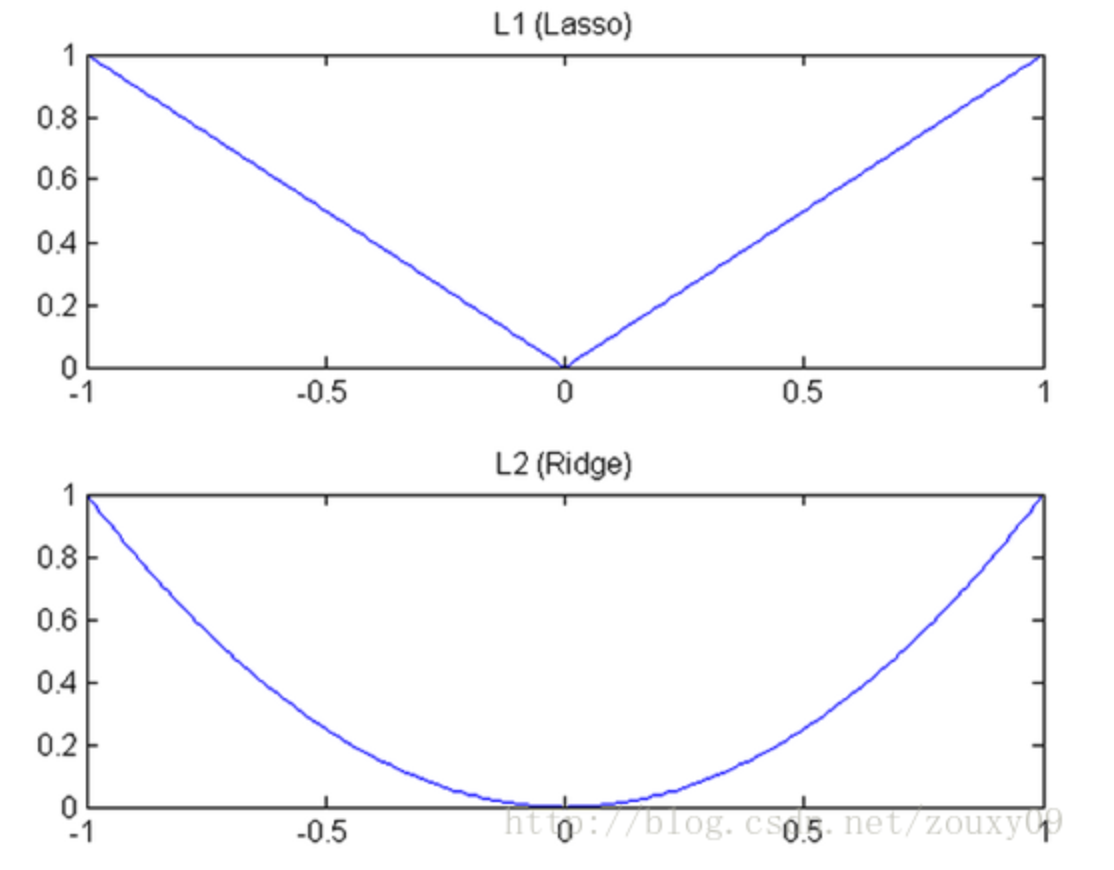
$l_1$和$l_2$在梯度下降中如图所示，$l_1$的下降速度在靠近0的时候非常快，所以会很快降到0。

★为什么L1、L2有如此区别以及L1、L2是怎么运作的？

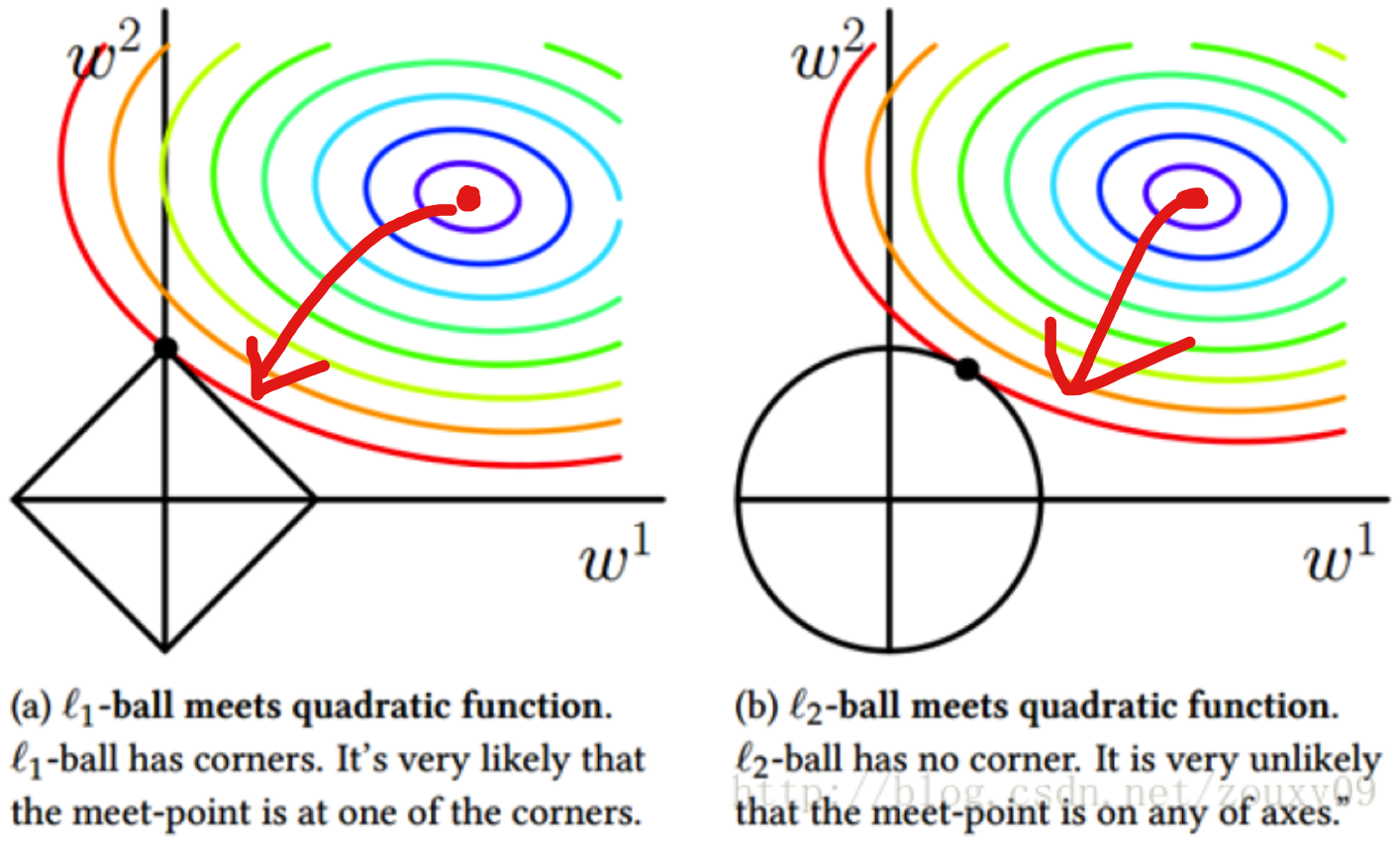
图形解释：

$$min\frac{1}{N}\sum_{i}^{N}{L(y_1,f(x_1)) }$$

为方便表示我们只考虑二维的平面，即$w_1,w_2$两个特征，在$w_1,w_2$平面内画出目标函数的等高线，这个等高线我们知道就是目标函数的碗投影在二维图中的表示。

$$\lambda J(f)$$

$l_2$正则项则成为平面上半径为C（这个C在sklearn的logistics中可以定义）的一个圆。

$l_1$正则项则成为平面上对角线一半为C的一个正方形。（这里省去$\lambda$而改用C，$\lambda=\frac{1}{C}$）

求解的intuition以及为什么可以防止过拟合1

我们知道碗（等高线）的optimal在最中心的地方，但是我们现在不要那个地方最拟合的解，我们要不那么完美的解，因此我们加入了正则项，把正则项的投影到图中，正则项最小的地方自然在原点处。

我们所希望的$w_1,w_2$ s.t. 正则项也小，损失函数也小，因此我们就在这里有一个trade off：

• C越大($\lambda$越小)，交点越靠近碗的optimal，惩罚程度越小，模型可能还是过拟合。
• C越小($\lambda$越大)，交点越靠近原点，惩罚程度越大，但是模型表现可能欠拟合。

可以看到$l_1$和$l_2$的不同之处在于$l_1$和坐标轴和坐标轴相交的地方有角，大部分的时候目标函数会和$l_1$在角处相交，而角处是有稀疏性的。

$l_2$因为没有角，所以相交在有稀疏性的地方概率很小。这样就直观的解释了为什么$l_1$可以产生稀疏性，$l_2$不可以产生稀疏性。

正则化为什么可以防止过拟合2

为了防止过拟合，我们要让经验风险最小化，正则化项也最小化，即让两者之和最小化

那么我们如何说明加入了这个正则项后，相较于$\hat{\bf{\beta}}$来说，$\widetilde{\bf{\beta}}$确实避免了过拟合呢？

因为从数学上可以证明，$\Vert \widetilde{\bf{\beta}} \Vert < \Vert \hat{\bf{\beta}} \Vert $，注意这里的小于是严格的小于。这个性质本身告诉了我们这样一个及其重要的本质：

加入正则项后，估计出的（向量）参数的长度变短了（数学上称为shrinkage）。

换句话说，长度变短了就意味着，向量$\widetilde{\bf{\beta}}$中的某些分量在总体程度上比$\hat{\bf{\beta}}$的分量变小了。极端来说，向量$\widetilde{\bf{\beta}}$中的某些分量可能（因为也可能是因为每个分量都变小一点点最后造成整体长度变小）被压缩到了0。

虽然这里其实还没有完整说明我们实现了避免过拟合，但至少从某种程度上说，加入正则项和的参数估计是符合我们之前的预定目标的，即用尽量少的变量去拟合数据。

在知乎上看到的解答：

向你的模型加入某些规则，加入先验，缩小解空间，减小求出错误解的可能性。你要把你的知识数学化告诉这个模型，对代价函数来说，就是加入对模型“长相”的惩罚. 损失一部分，让模型无法完美的拟合

总结

因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

ref: http://blog.csdn.net/zouxy09/article/details/24971995

Coursea: Machine Learning

&Phd罗.