cost function

Cost Function与Gradient Descent

1. 定义

为了在假设空间中选取最优的模型，引入了损失函数和风险函数，损失函数度量模型一次预测的好坏，风险函数度量了平均意义下模型预测的好坏。

我们知道监督学习是在假设空间里选出模型$f$作为决策函数，对于给定的输入x，由$f(x)$给出相应的$Y$，这个输出值可能与真实值不一致，因此需要有一个损失函数（cost function）去度量错误的程度。

常见的损失函数有如下几种：

1. 0-1 loss function:

   $$L(Y,f(x))=\begin{equation} \left\{ \begin{array}{lr} 1, & Y\neq f(x)\\ 0, & Y= f(x)\\ \end{array} \right. \end{equation}$$

2. 平方损失函数:

   $$L(Y,f(X))=(Y-f(X))^2$$

3. 绝对值损失函数:

   $$L(Y,f(X))=|Y-f(x)|$$

4. 对数损失函数(对数似然损失函数)

   $$L(Y,P(Y|X))=-logP(Y|X)$$

   损失函数值越小，模型越好。

2. 应用线性回归

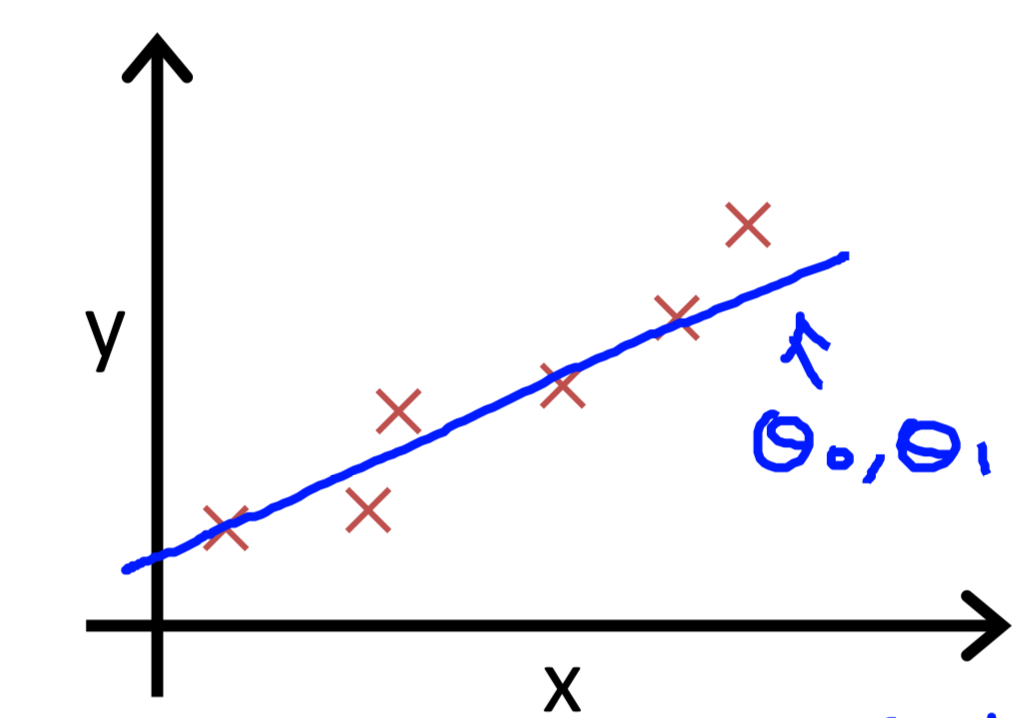
线性回归：$y=\theta_0+ \theta_1x$

我们首先看看在线性回归中，损失函数是如何应用的，我们选择了最简单的一元线性回归。在这里选择了平方损失函数，损失函数如下：

$$J(\theta_0, \theta_1) = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left ( \hat{y}_{i}- y_{i} \right)^2 = \dfrac {1}{2m} \displaystyle \sum _{i=1}^m \left (h_\theta (x_{i}) - y_{i} \right)^2$$

​ 参数解释：求出每个训练样本的平方损失值并求和，其中$\hat{y}{i},h\theta (x{i})$是预测值，$y{i} $是真实值。

​ m是训练样本的数量。数量越多误差越大，所以平滑一下。2则是在求解偏导中会约分的值，为了让下降更平滑。

最简单的情况：

当我们有训练样本(1,1),(2,2),(3,3)，并选择$\theta_0=0$，只考虑$\theta_1(斜率)$的变化对于损失函数值的影响。如下图：

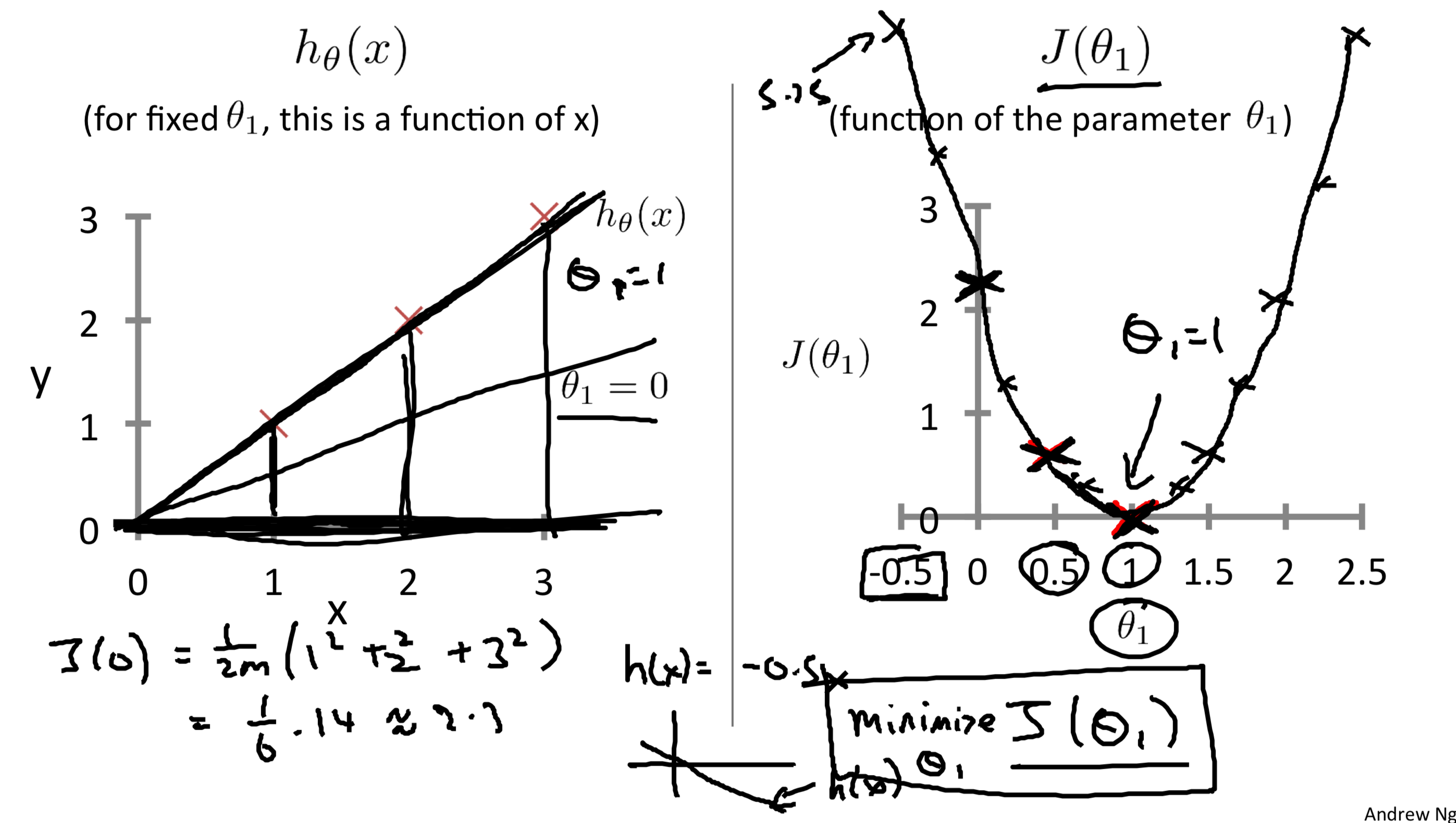
其中左图是训练样本和斜率=1，0.5，0时的情况，右图是损失函数的值。

求出右图的公式非常简单:

$$J=\frac{14(\theta_1-1)^2}{6}$$

通过简单的计算我们可以得知$J(1)=0,J(0)=2.3$，观察右图中损失函数的值，我们可以知道，损失函数最优的情况是当斜率为1时，损失=0，由于是只考察单个参数，所以呈抛物线的形状。

当斜率越往1靠近时，损失值就越小。

稍复杂的情况

当我们将$\theta_0$也考虑进来的时候，损失函数就不是一个抛物线这么简单了。会呈现一个碗形。

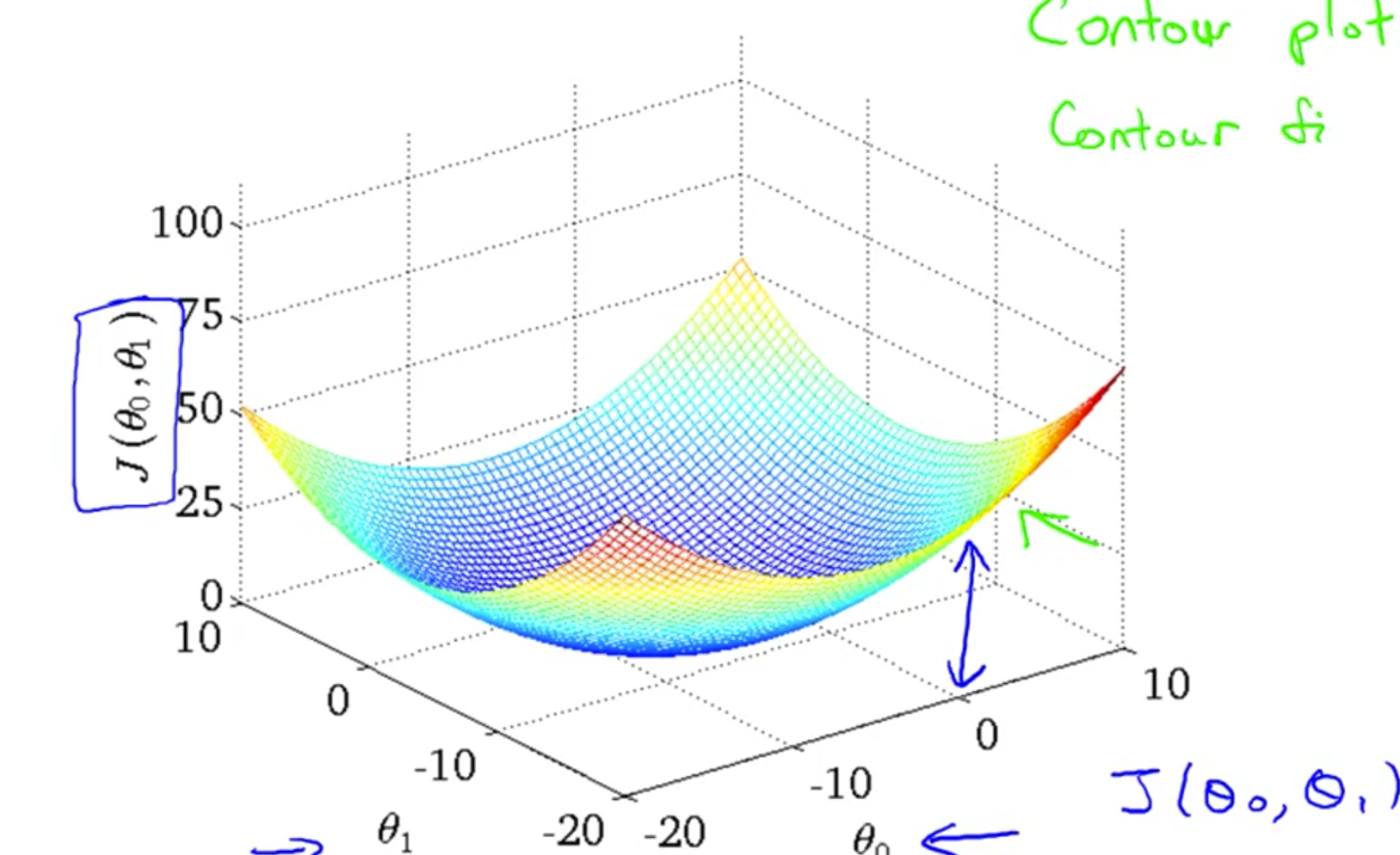
那这个时候我们怎么求解到损失函数的最小值呢？接下来就要使用一种梯度下降的方式。梯度下降在很多情况下都是十分有用的。

损失函数求解：Gradient descent

Big picture：梯度下降是用来得到损失函数的local minimum的，我们应该沿着值下降的路线走，即我们应该沿着斜率为负的方向走。

intuition：沿着损失函数下降的方向走路，每次跨出的步长/梯度都不一样

梯度下降的公式：

$$\theta_1:=\theta_1-\alpha \frac{d}{d\theta_1} J(\theta_1)$$

参数解释：$\alpha$，学习速率；$\theta_1$，参数；$ \frac{d}{d\theta_1} J(\theta_1)d$，求偏导。

从公式我们可以看出，步长项$\alpha \frac{d}{d\theta_1} J(\theta_1)$是取了损失函数对某个参数的偏导数再乘上$\alpha$，学习速率，取负号，加上原来的值。

参数更新：

用Gradient descent求解Linear Regression的系数

$$\begin{align*} \text{repeat until convergence: } \lbrace & \newline \theta_0 := & \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}(h_\theta(x_{i}) - y_{i}) \newline \theta_1 := & \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}\left((h_\theta(x_{i}) - y_{i}) x_{i}\right) \newline \rbrace& \end{align*}$$

在这里要注意参数$\theta_1,\theta_0$是同时更新的:

为什么要取负号的intuition：由于梯度下降是要找到local minimum。

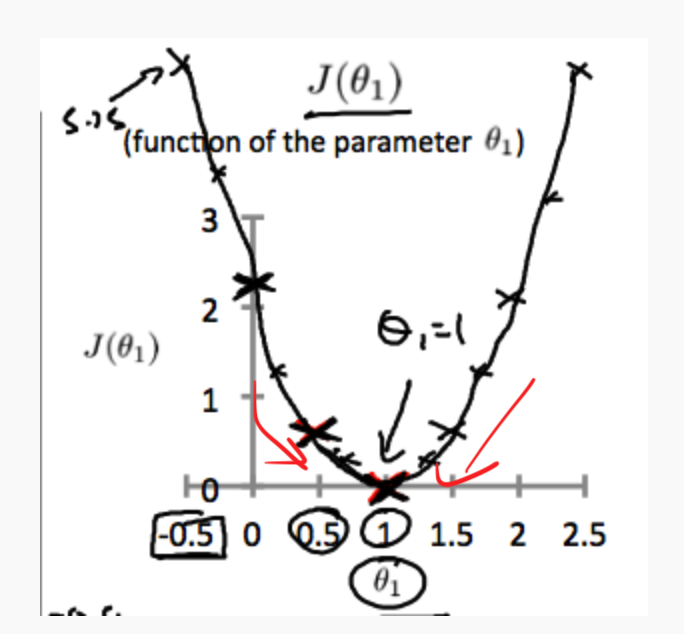
所以如图

• 如果斜率是正的，那应该减小$\theta_1$，因此加上负号，步长变负。
• 如果斜率是负的，那应该增大$\theta_1$，因此加上符合，步长变正。

关于步长的长度：步长与斜率正相关。

步长长度由$\alpha$和$|斜率|$决定，$|斜率|$越大的地方，离local minimum必然越远，因此步长应该大大，而在$|斜率|$越小的地方，离local minimum必然越近，因此步长应该较小。在这我们不用去更改学习速率，因为$|斜率|$本身告诉了我们步长的幅度应该是多大。

关于$\alpha$的大小：

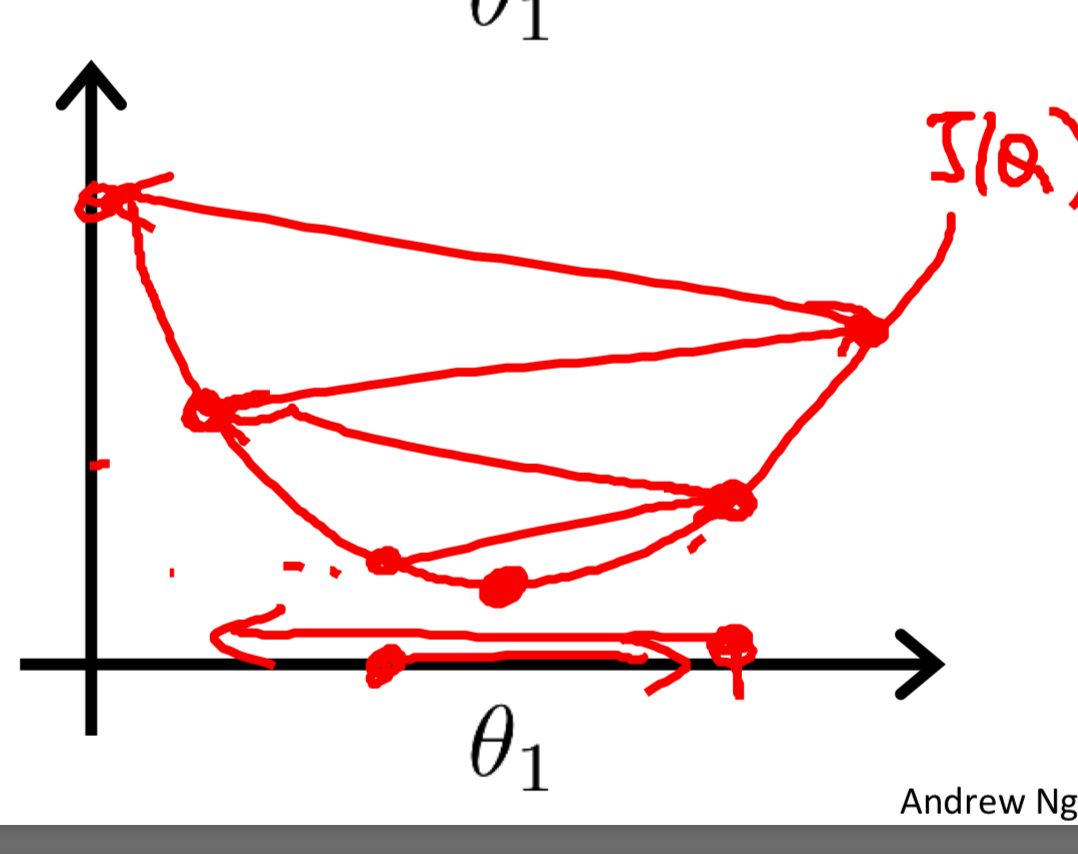
如果$\alpha$过大，那么步长相应的会变大，下山太快就找不到最低处，可能找不到这样有可能会跨过local minimum，甚至无法拟合。

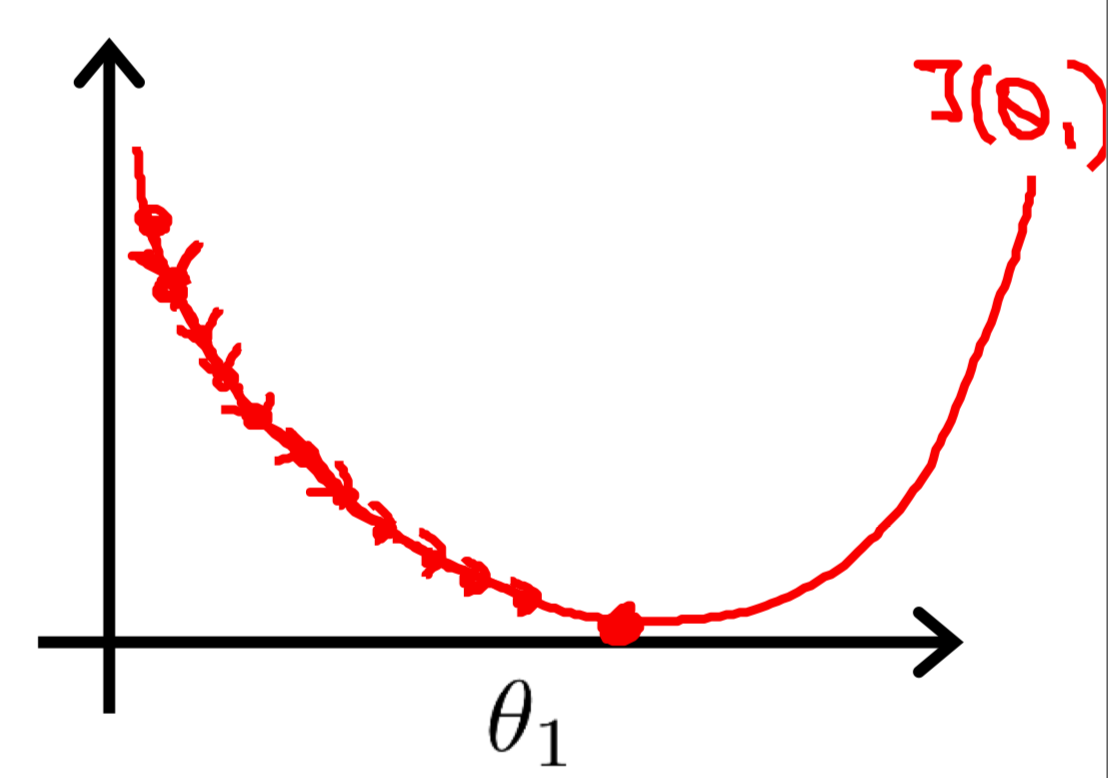
如果$\alpha$过小，那么步长相应的会变小，下山太慢时间太久，这样下降速度会变慢，算法效率很低。

梯度下降的起点：

梯度下降的起点（一般选参数都为0开始）选择不同，结果也会不同：

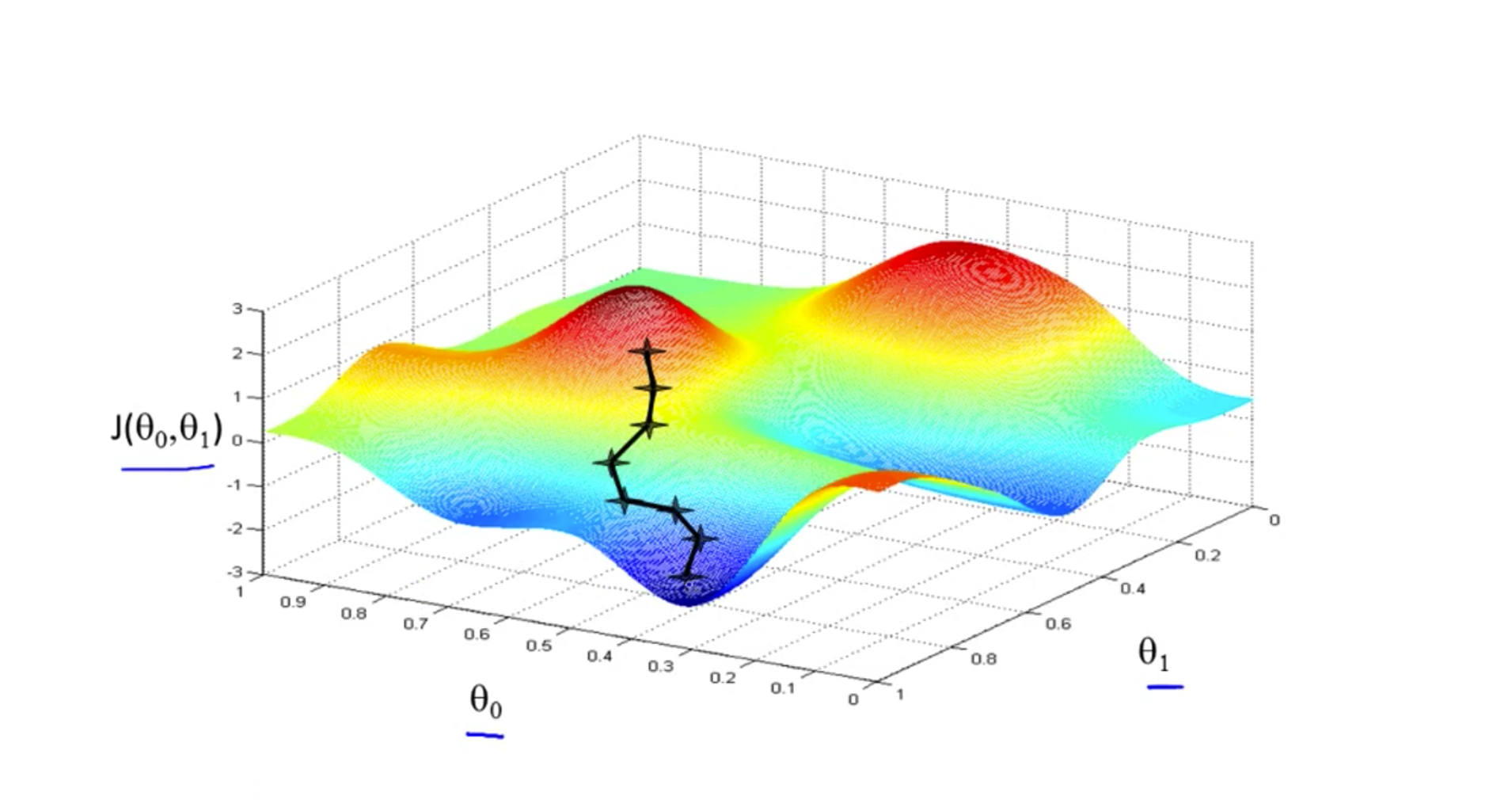
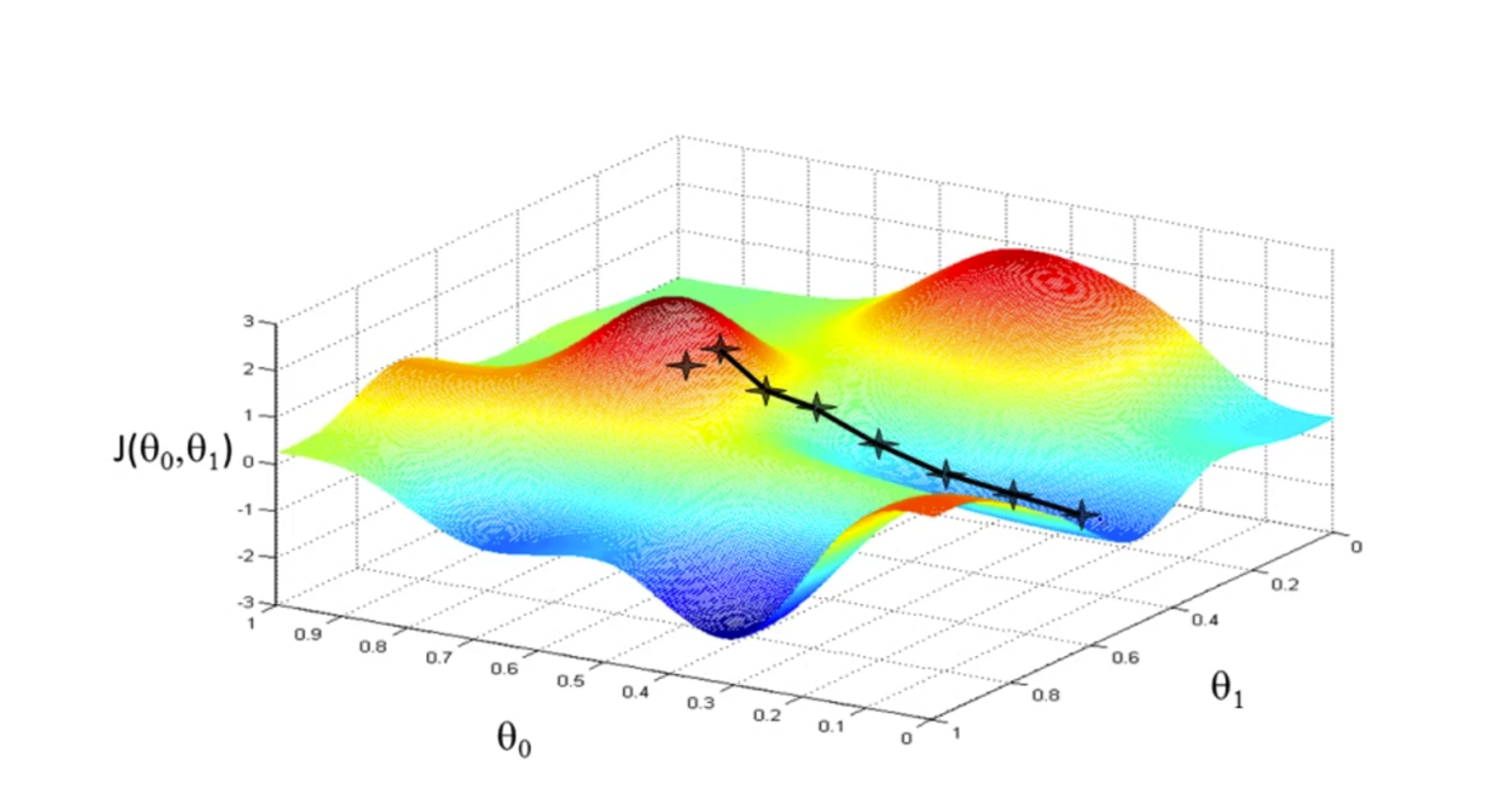
这也是我比较困惑的地方。

算法复杂度：$O(mn)$ m: train data size, n: 特征数量+1

训练数据大小对于梯度下降的影响：在这种梯度下降的方法(batch Gradient Descent)中，我们使用所有的训练数据去进行每次计算，因此如果训练数据过大，即m过大，计算时间很长。

因此有人提出了一个梯度下降算法的改进版SGD(随机梯度下降)。重点在随机上，该算法在每次计算梯度的时候只随机选取部分数据来计算，涉及参数miniBatchSize，定义了抽样的数据比例，为了保证所有数据都参与了计算，miniBatchSize * iteration最好 > 1.

总结

损失函数是用来度量在某组参数下，模型的好坏程度，反过来也是我们用来选择参数的方法，而这个参数的选择是无限种可能的，因此我们必须选择一种理性的方法去得到最优的参数—— 梯度下降。梯度下降中参数会往损失函数减小的方向改变，直到到达local minimum为止。

Reference:

https://www.jianshu.com/p/1e7558e18e73

Andrew Ng. Machine Learning.

李航《统计方法学》.